Appendix D - Classifying iris flowers
Goal
The goal of this page is to provide a very short demo of a tidymodels
pipeline for model development and assessment of predictive capacity. We
will use a subset of the iris data (only for 2 species),
where we will fit a kernel SVM (or radial basis
function SVM) using the svm_rbf interface with the
default kernlab engine. We will first split the data into a
test and model development part, where afterwards we
will use v-fold cross validation to split the model development
part into training and validation datasets (v
times). The model parameters will be trained on the training dataset,
whereas the validation dataset will be used for hyperparameter tuning.
After finding the best combination of hyperparameters, the full model
development set will be used to fit the final model, which will then be
predicted on the left out test dataset and predictive
performance will be quantified.
Let’s load the needed libraries and set the seed to make the script fully reproducible (i.e. running it multiple times will result in the same result, including random sampling):
library(tidyverse)
library(tidymodels)
library(kernlab)
set.seed(1234567)Preparation of data
Let’s retrieve a subset of the iris dataset, using only
2 of the 3 species (so that we can do binary classification):
dat <- iris %>%
as_tibble() %>%
filter(Species != "setosa") %>%
mutate(Species = droplevels(Species))
dat## # A tibble: 100 × 5
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## <dbl> <dbl> <dbl> <dbl> <fct>
## 1 7 3.2 4.7 1.4 versicolor
## 2 6.4 3.2 4.5 1.5 versicolor
## 3 6.9 3.1 4.9 1.5 versicolor
## 4 5.5 2.3 4 1.3 versicolor
## 5 6.5 2.8 4.6 1.5 versicolor
## 6 5.7 2.8 4.5 1.3 versicolor
## 7 6.3 3.3 4.7 1.6 versicolor
## 8 4.9 2.4 3.3 1 versicolor
## 9 6.6 2.9 4.6 1.3 versicolor
## 10 5.2 2.7 3.9 1.4 versicolor
## # ℹ 90 more rowsdat %>% count(Species)## # A tibble: 2 × 2
## Species n
## <fct> <int>
## 1 versicolor 50
## 2 virginica 50Set division
We first split the data into a model development part and a testing part, where we reserve 75% of the records for the model development part:
main_split <- initial_split(dat, prop = 3/4)
main_split## <Training/Testing/Total>
## <75/25/100>Then, we will split the model development part of the main datasplit further for v-fold (here v = 3) cross validation:
val_split <- vfold_cv(training(main_split), v = 3)
val_split## # 3-fold cross-validation
## # A tibble: 3 × 2
## splits id
## <list> <chr>
## 1 <split [50/25]> Fold1
## 2 <split [50/25]> Fold2
## 3 <split [50/25]> Fold3Define the workflow
We define a data recipe specification, without prepping it
(which will later be done automatically). The recipe specifies which
column is the response (the “Species” column) and which columns are the
predictors (the other columns, as indicated by the .).
Then, it adds a data preprocessing step, specifying that all numeric
predictors should be normalized to zero mean and unit variance:
dat_rec <- dat %>%
recipe(Species ~ .) %>%
step_normalize(all_numeric_predictors())We also define the model specification, including the hyperparameters that need tuning, and set the engine:
svm_spec <- svm_rbf(mode = "classification",
cost = tune(),
rbf_sigma = tune()) %>%
set_engine("kernlab")Then, we bundle the data recipe and the model specification into a workflow object:
svm_wf <- workflow() %>%
add_recipe(dat_rec) %>%
add_model(svm_spec)To check the result:
svm_wf## ══ Workflow ═══════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: svm_rbf()
##
## ── Preprocessor ───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
## 1 Recipe Step
##
## • step_normalize()
##
## ── Model ──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
## Radial Basis Function Support Vector Machine Model Specification (classification)
##
## Main Arguments:
## cost = tune()
## rbf_sigma = tune()
##
## Computational engine: kernlabHyperparameter tuning
We first will specify a “grid” of hyperparameter values for which to
assess model fit on the validation dataset. The grid will consist of the
two parameters that we specified above need tuning:
rbf_sigma and cost, using functions with the
same name. We can look at the trans arguments in these
functions to see that the hyperparameter rbf_sigma will be
sampled in levels values between the specified range on a
log10 scale, where the values for cost will by default be
sampled on a log2 scale (hence the range -6 to 4 for
rbf_sigma and -8 to 9 for cost).
svm_grid <- grid_regular(
rbf_sigma(range = c(-6,4)),
cost(range = c(-8,9)),
levels = 10)To explore, we could show the grid:
svm_grid## # A tibble: 100 × 2
## rbf_sigma cost
## <dbl> <dbl>
## 1 0.000001 0.00391
## 2 0.0000129 0.00391
## 3 0.000167 0.00391
## 4 0.00215 0.00391
## 5 0.0278 0.00391
## 6 0.359 0.00391
## 7 4.64 0.00391
## 8 59.9 0.00391
## 9 774. 0.00391
## 10 10000 0.00391
## # ℹ 90 more rowsunique(svm_grid$rbf_sigma)## [1] 1.000000e-06 1.291550e-05 1.668101e-04 2.154435e-03 2.782559e-02 3.593814e-01 4.641589e+00 5.994843e+01 7.742637e+02 1.000000e+04unique(svm_grid$cost)## [1] 0.00390625 0.01446679 0.05357775 0.19842513 0.73486725 2.72158000 10.07936840 37.32892927 138.24764658 512.00000000We see that there are now 100 combinations (10 x 10).
We then tune the hyperparameters using the tune_grid
function, passing in the workflow object, the object specifying the
v-fold train-validation splits, and the object containing the
grid to be sampled:
svm_res <- svm_wf %>%
tune_grid(resamples = val_split,
grid = svm_grid)We can retrieve the combination of hyperparameter that gives the best
average performance on the validation dataset using the
select_best function, where we need to indicate according
to which metric we judge the performance of the candidate models (here
according to the ROC-AUC metric):
svm_best <- svm_res %>%
select_best(metric = "roc_auc")
svm_best## # A tibble: 1 × 3
## cost rbf_sigma .config
## <dbl> <dbl> <chr>
## 1 2.72 0.0278 Preprocessor1_Model055We can visualize the fitted grid with the best hyperparameter combination indicated:
svm_res %>%
collect_metrics() %>%
filter(.metric == "roc_auc") %>%
ggplot() +
geom_contour_filled(mapping = aes(x = rbf_sigma,
y = cost,
z = mean),
bins = 20) +
geom_point(data = svm_best,
mapping = aes(x = rbf_sigma,
y = cost)) +
scale_y_log10() +
scale_x_log10() +
labs(x = "Sigma", y = "Cost")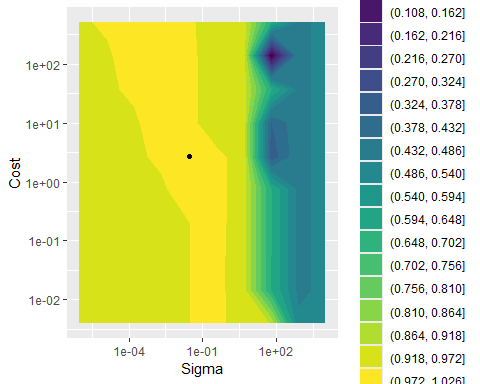
Testing predictive performance
After having tuned the hyperparameters, we can use all data that was
used during the hyperparameter tuning (thus: all folds with training and
validation data) to fit the final model (with the selected
hyperparameter values). For this we can use the
finalize_model function to update the model-specification
with these best hyperparameters:
svm_final <- svm_spec %>%
finalize_model(svm_best)Likewise, we can update the workflow by updating the finalized model:
svm_wf_final <- svm_wf %>%
update_model(svm_final)We can check the steps above by inspecting the updated final workflow:
svm_wf_final## ══ Workflow ═══════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: svm_rbf()
##
## ── Preprocessor ───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
## 1 Recipe Step
##
## • step_normalize()
##
## ── Model ──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
## Radial Basis Function Support Vector Machine Model Specification (classification)
##
## Main Arguments:
## cost = 2.72158000034875
## rbf_sigma = 0.0278255940220713
##
## Computational engine: kernlabTo perform a last fit of the model based on all training data, and
predict on the testing data (that has not been used during any model
development), we can then use the last_fit function:
svm_final_fit <- svm_wf_final %>%
last_fit(main_split)We can compute predictive performance metrics (thus: on the test
dataset) using the collect_metrics function:
svm_final_fit %>%
collect_metrics()## # A tibble: 3 × 4
## .metric .estimator .estimate .config
## <chr> <chr> <dbl> <chr>
## 1 accuracy binary 0.96 Preprocessor1_Model1
## 2 roc_auc binary 0.994 Preprocessor1_Model1
## 3 brier_class binary 0.0277 Preprocessor1_Model1Using the collect_predictions function we can retrieve
the predictions on the test dataset, and from this we can then retrieve
the confusion matrix:
svm_final_fit %>%
collect_predictions() %>%
conf_mat(truth = Species,
estimate = .pred_class)## Truth
## Prediction versicolor virginica
## versicolor 12 0
## virginica 1 12We see that the test dataset contains 25 records (25% of the 100 records we started with). The model fitted and tuned on the other 75% of the data predicts quite well on this test dataset: of the 25 records, 24 were correctly classified (96% accuracy)!