This tells us that the coordinate indexing of images always starts in the top left corner (instead of the bottom left as ggplot assumes).
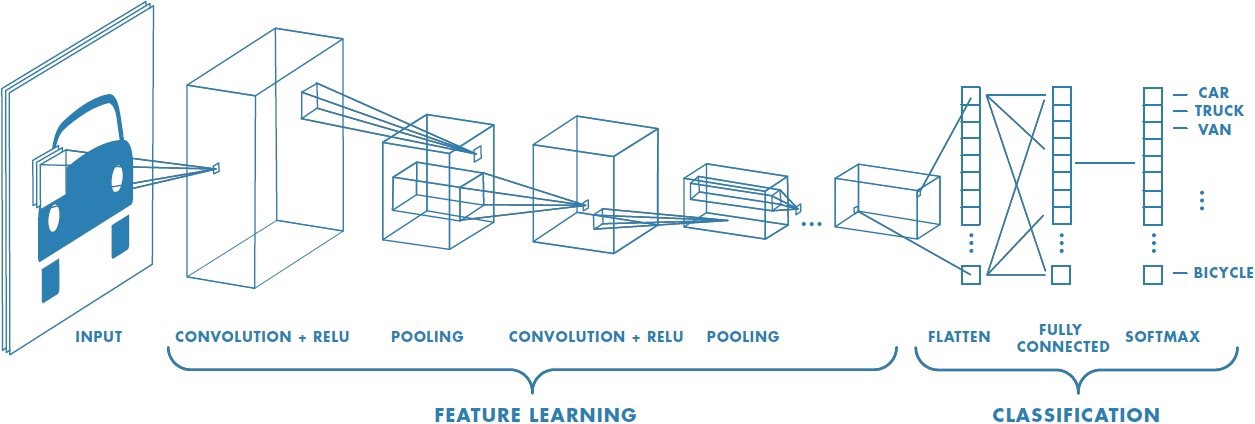
Understanding convolutional neural networks
Today’s goal: to understand the steps of a Convolutional Neural Network (CNN)
1 Introduction
In this practical you will “manually” follow the steps of a Convolutional Neural Network (CNN) yourself. Note that in this practical we will not actually train a CNN, but just go through the various underlying layer types to get a feeling about what happens “under the hood” of a CNN.
We will take two small top-down images of a grass pasture and a forest as an example for this practical. We will showcase with some simple filters and pooling that we can distinguish the two images and finally come to a grass- and forest-probability for both images. This practical is aimed at familiarizing yourself with the working of a CNN, but it is not aimed at improving your coding skills per se. That is why many R scripts are provided to you.
2 Setting up
Start by downloading the grass.jpg and
forest.jpg files from Brightspace > Image analyses
> Data > Images 2, save them in a new directory that you
intend to use for this practical (e.g. data / raw /
images2.
To load in the images, mutate and plot them we need the
tidyverse, imager, gridExtra and
scales packages. Install the packages if needed and then
load them.
cimg
objects. # Load libraries
library(tidyverse)
library(imager)
library(gridExtra)
library(scales)
# load images
grass <- load.image("data/raw/images2/grass.jpg")
forest <- load.image("data/raw/images2/forest.jpg")3 Exploration
str function. str(grass)## 'cimg' num [1:50, 1:50, 1, 1:3] 0.1961 0.3843 0.4902 0.451 0.0549 ...str(forest)## 'cimg' num [1:50, 1:50, 1, 1:3] 0.478 0.58 0.624 0.671 0.584 ...We can also plot the images to see what they look like in R. You can do this either in base R or with ggplot. When you use ggplot you first need to convert the arrays to data.frames or tibbles and convert the RGB values to the corresponding hexadecimal colour code (column “colCode”).
grassdf <- as.data.frame(grass, wide = "c") %>%
as_tibble() %>%
mutate(colCode = rgb(c.1, c.2, c.3))
grassdf## # A tibble: 2,500 × 6
## x y c.1 c.2 c.3 colCode
## <int> <int> <dbl> <dbl> <dbl> <chr>
## 1 1 1 0.196 0.4 0 #326600
## 2 2 1 0.384 0.6 0.0275 #629907
## 3 3 1 0.490 0.694 0.0667 #7DB111
## 4 4 1 0.451 0.6 0.133 #739922
## 5 5 1 0.0549 0.157 0 #0E2800
## 6 6 1 0.110 0.239 0.0235 #1C3D06
## 7 7 1 0.314 0.518 0.0941 #508418
## 8 8 1 0.349 0.592 0 #599700
## 9 9 1 0.337 0.545 0 #568B00
## 10 10 1 0.384 0.529 0.0235 #628706
## # ℹ 2,490 more rowsforestdf <- as.data.frame(forest, wide = "c") %>%
as_tibble() %>%
mutate(colCode = rgb(c.1, c.2, c.3))
forestdf## # A tibble: 2,500 × 6
## x y c.1 c.2 c.3 colCode
## <int> <int> <dbl> <dbl> <dbl> <chr>
## 1 1 1 0.478 0.655 0.282 #7AA748
## 2 2 1 0.580 0.765 0.388 #94C363
## 3 3 1 0.624 0.808 0.431 #9FCE6E
## 4 4 1 0.671 0.855 0.478 #ABDA7A
## 5 5 1 0.584 0.773 0.384 #95C562
## 6 6 1 0.624 0.812 0.412 #9FCF69
## 7 7 1 0.631 0.816 0.4 #A1D066
## 8 8 1 0.631 0.820 0.392 #A1D164
## 9 9 1 0.627 0.816 0.384 #A0D062
## 10 10 1 0.545 0.733 0.294 #8BBB4B
## # ℹ 2,490 more rowsHere, we first convert the objects grass and
forest into a data.frame, which includes the ‘x’ and ‘y’
value of the position of each pixel, and where the values of the 3
layers (R, G and B) will be stored in columns that will be named ‘c.1’,
‘c.2’ and ‘c.3’ (see the prefix “c” passed on to the argument
wide). Then, the values of columns ‘c.1’, ‘c.2’ and ‘c.3’
are used to get a hexidecimal colour code using the function
rgb. We can now plot the images:
p1 <- ggplot(data = grassdf,
mapping = aes(x = x, y = y)) +
geom_raster(aes(fill = colCode)) +
scale_fill_identity() +
ggtitle("Grass")
p2 <- ggplot(data = forestdf,
mapping = aes(x = x, y = y)) +
geom_raster(aes(fill = colCode)) +
scale_fill_identity() +
ggtitle("Forest")
grid.arrange(p1, p2, nrow = 1)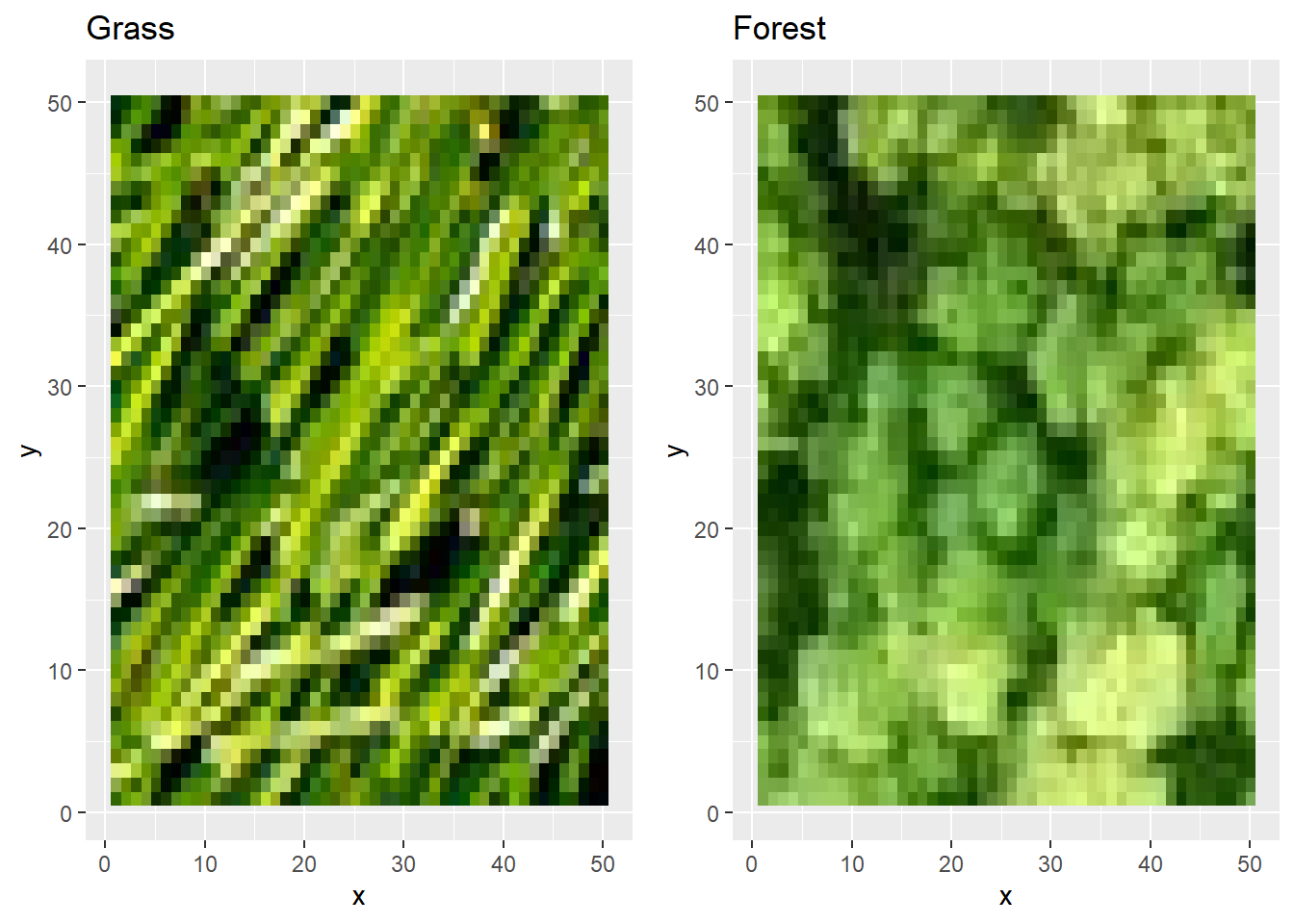
If you compare these plots to the actual images (e.g., when you open them with Windows viewer) you’ll notice that these are plotted upside-down.
We can fix the upside-down-plotting by reversing the y axis of the plots.
p1 <- p1 +
scale_y_continuous(trans = scales::reverse_trans())
p2 <- p2 +
scale_y_continuous(trans = scales::reverse_trans())
grid.arrange(p1, p2, nrow = 1)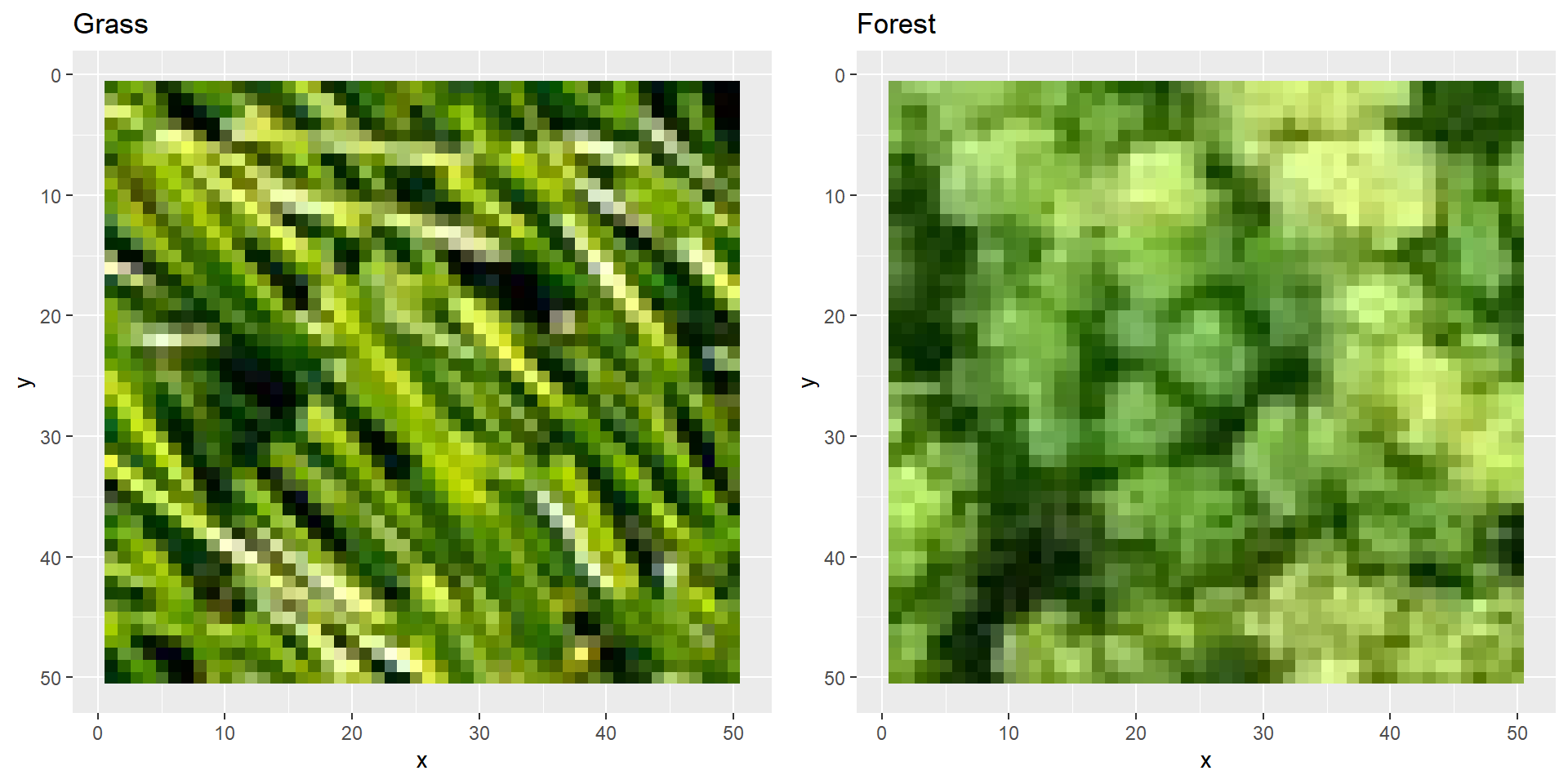
That’s more like it!
4 Pre-process
In real-life CNNs all the three colour channels (R,G,B) are often
used as input data. However, for the sake of simplicity and because our
two images are probably easily distinguishable, let’s convert these
three colour channels to one dimension: grayscale.
grass <- grayscale(grass)
forest <- grayscale(forest)Let’s plot these images again.
We now need to use the grey function instead of the
rgb function to convert the colour values to hexadecimal
colour codes.
If we’re going to plot transformed versions of these images more
often it will require a lot of repetitive code every time. So… let’s
first make a function for it and then apply it to the converted images:
we call this name this function plotBoth. We will make sure
to scale the grey values before converting it to hexadecimal code,
because later on during the transformation layers these values can
become larger than 1. We do this by dividing the values by the maximum
value across the images. We define the function such that it plots 2
greyscale images next to each other (grass and forest):
plotBoth <- function(grass, forest) {
# Get max values across both images
maxv <- max(grass, forest)
# Convert to tibble
grassdf <- grass %>%
as.data.frame() %>%
as_tibble() %>%
mutate(colCode = value / maxv, # now max is 1
colCode = grey(colCode))
forestdf = forest %>%
as.data.frame() %>%
as_tibble() %>%
mutate(colCode = value / maxv,
colCode = grey(colCode))
# Create plots
p1 <- ggplot(data = grassdf,
mapping = aes(x = x, y = y)) +
geom_raster(aes(fill = colCode)) +
scale_fill_identity() +
ggtitle("Grass") +
scale_y_continuous(trans = scales::reverse_trans())
p2 <- ggplot(data = forestdf,
mapping = aes(x = x, y = y)) +
geom_raster(aes(fill = colCode)) +
scale_fill_identity() +
ggtitle("Forest") +
scale_y_continuous(trans = scales::reverse_trans())
# Plot both images
grid.arrange(p1, p2, nrow = 1)
}Let’s test the function by plotting both images next to each other using the function defined above:
plotBoth(grass, forest)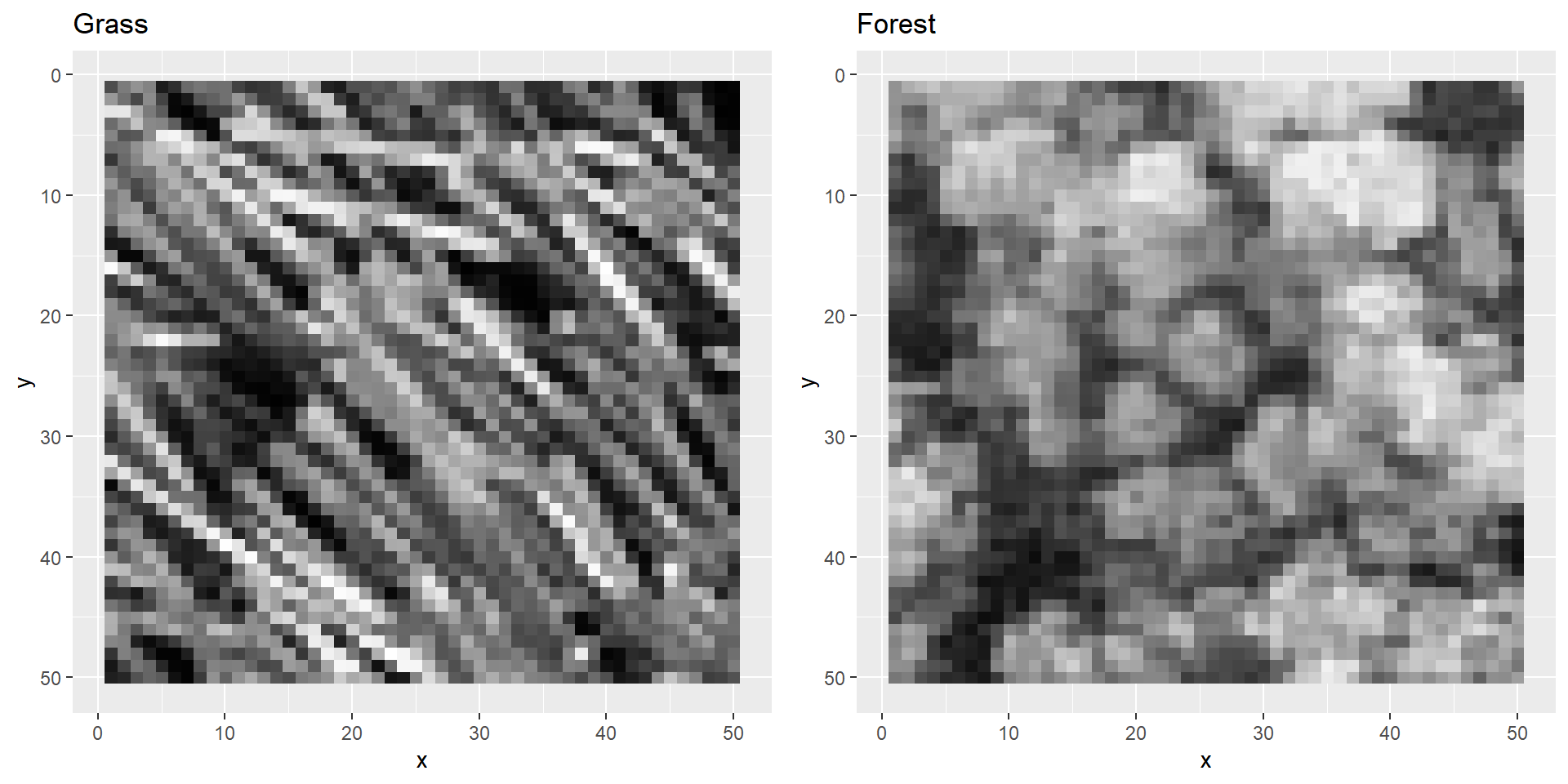
Now we are ready to put our input layers into the CNN. Remember that in this practical we imagine that we have already trained a very simple CNN and that we are going through the steps of how this CNN computes the class probabilities for each image you feed into it.
5 Layers
5.1 Convolution
The first layer of a CNN is often a Convolution Layer. The naming is actually a bit misleading, because mathematically this layer is not performing convolution. What this layer technically does is performing a sliding sum of element-wise matrix multiplications with multiple convolution filters, so more like a dot product. For one simple convolution filter (in yellow) and a very small image (green) this process is visualized in this animation:

The convolved value of each sliding window step will be assigned to the center element of the convolution filter. This means that you’ll lose rows and columns at the edges of your image. If you use a larger convolution filter then you’ll lose more rows and columns than in this example. If the sliding filter moves with strides greater than 1 than the resulting convolved feature will be even smaller.
The filters that are used during convolution are trained during the epochs of training your CNN. If you put multiple layers of convolution after each other the CNN is able to extract more and more complicated features from the image. However, our images are actually quite easily distinguishable with only one filter.
The grass has more edges than the trees. An edge-detection filter will therefore most likely work well as a first step to distinguish both images. Of course, other filters might also perform well or even better.
Now that we got a feeling for which filter type will be useful for distinguishing grass from forest, let’s create three of them. Again, note that these filters are in practice trained values and you don’t have to come up with them yourself. For some common first-order convolutional filters see this Wikipedia page.
flt1 <- matrix(c(1, 0,-1,
0, 0, 0,
-1, 0, 1),
ncol = 3)
flt1## [,1] [,2] [,3]
## [1,] 1 0 -1
## [2,] 0 0 0
## [3,] -1 0 1flt2 <- matrix(c(0, 1, 0,
1,-4, 1,
0, 1, 0),
ncol = 3)
flt2## [,1] [,2] [,3]
## [1,] 0 1 0
## [2,] 1 -4 1
## [3,] 0 1 0flt3 <- matrix(c(-1,-1,-1,
-1, 8,-1,
-1,-1,-1),
ncol = 3)
flt3## [,1] [,2] [,3]
## [1,] -1 -1 -1
## [2,] -1 8 -1
## [3,] -1 -1 -1flt1 <- as.cimg(flt1)
flt2 <- as.cimg(flt2)
flt3 <- as.cimg(flt3)Okay, let’s actually perform the convolution. Take again a good look
at the convolution animation to understand what is computed during this
operation. To compute to convolution of an image with a certain filter
you can use the convolve function of the imager
package. Note that this function automatically applies some padding
around the image to make sure that the convolved image has the same
number of pixels as the original (in this case 50x50px). The “basic”
convolution operation does not do that and would return a 48x48px image,
because our filters are 3x3px we lose 2 rows and 2 columns at the edges.
In a CNN you can choose to apply padding or not.
grass1,
grass2, grass3, forest1,
forest2, forest3. # Apply filters on grass image
grass1 <- imager::convolve(im = grass, filter = flt1)
grass2 <- imager::convolve(im = grass, filter = flt2)
grass3 <- imager::convolve(im = grass, filter = flt3)
# Apply filters on forest image
forest1 <- imager::convolve(im = forest, filter = flt1)
forest2 <- imager::convolve(im = forest, filter = flt2)
forest3 <- imager::convolve(im = forest, filter = flt3)5.2 ReLU
Maybe you’ve tried to plot the convolved images after the next step and encountered an error. Well done! Because this is partly why we first need to perform a next step. The convolution layers are often followed by an activation function before giving the output of the nodes to the next layers. A common activation function that is often used is the ReLU function (rectified linear unit). What this layer basically does is setting all negative values of your convolved images to zero.
Suppose that you have a vector x with values -10, -9, …,
9, 10, then you can apply the ReLu filter yourself on a copy of
x (y) by setting all negative values to a
value 0:
x <- -10:10
y <- x
y[y < 0] <- 0
plot(x, y, type = "b")
This makes the computation and fitting of your CNN much more efficient.
plotBoth function to take a look at them. grass1[grass1 < 0] <- 0
forest1[forest1 < 0] <- 0
plotBoth(grass1, forest1)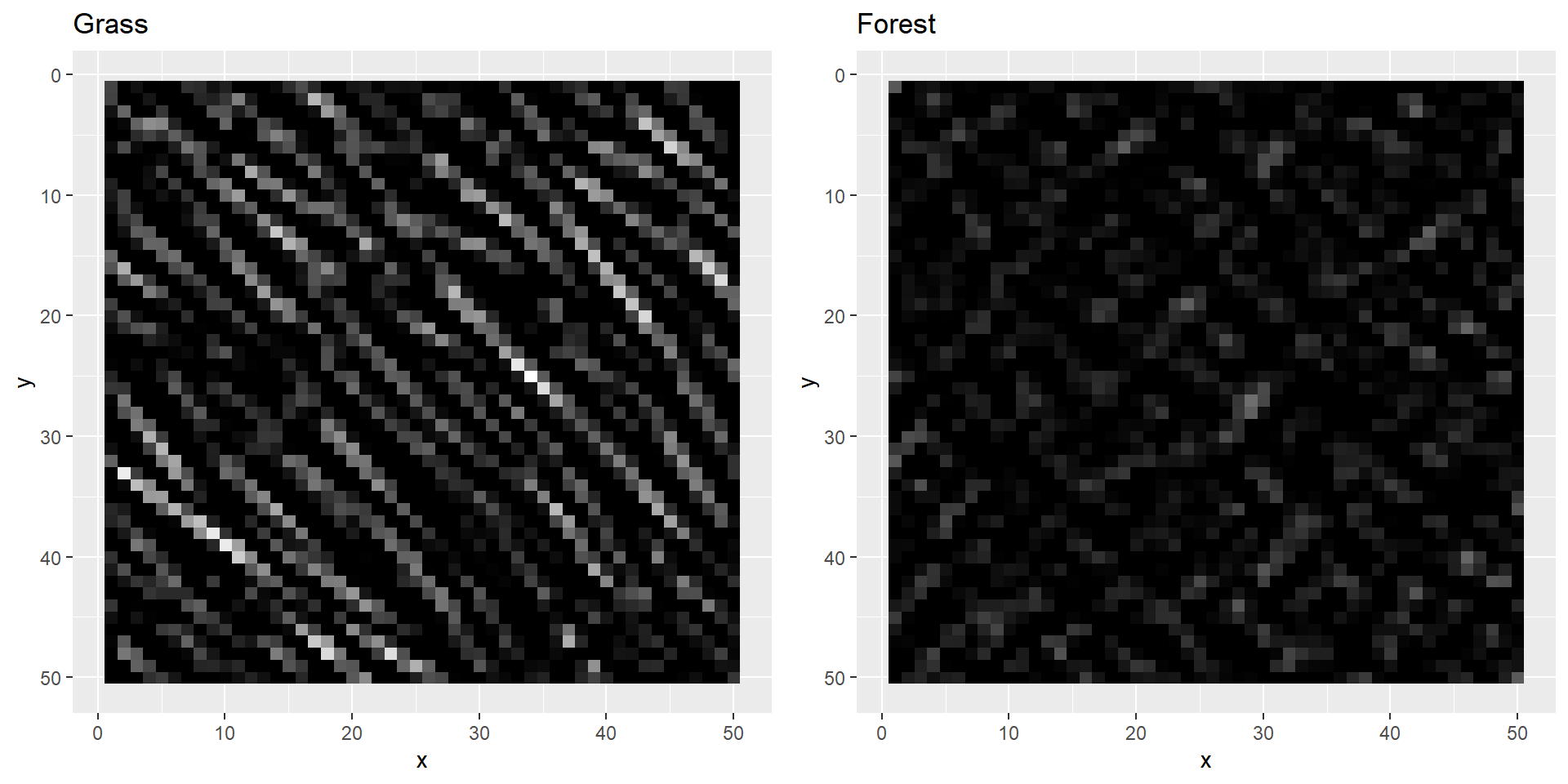
grass2[grass2 < 0] <- 0
forest2[forest2 < 0] <- 0
plotBoth(grass2, forest2)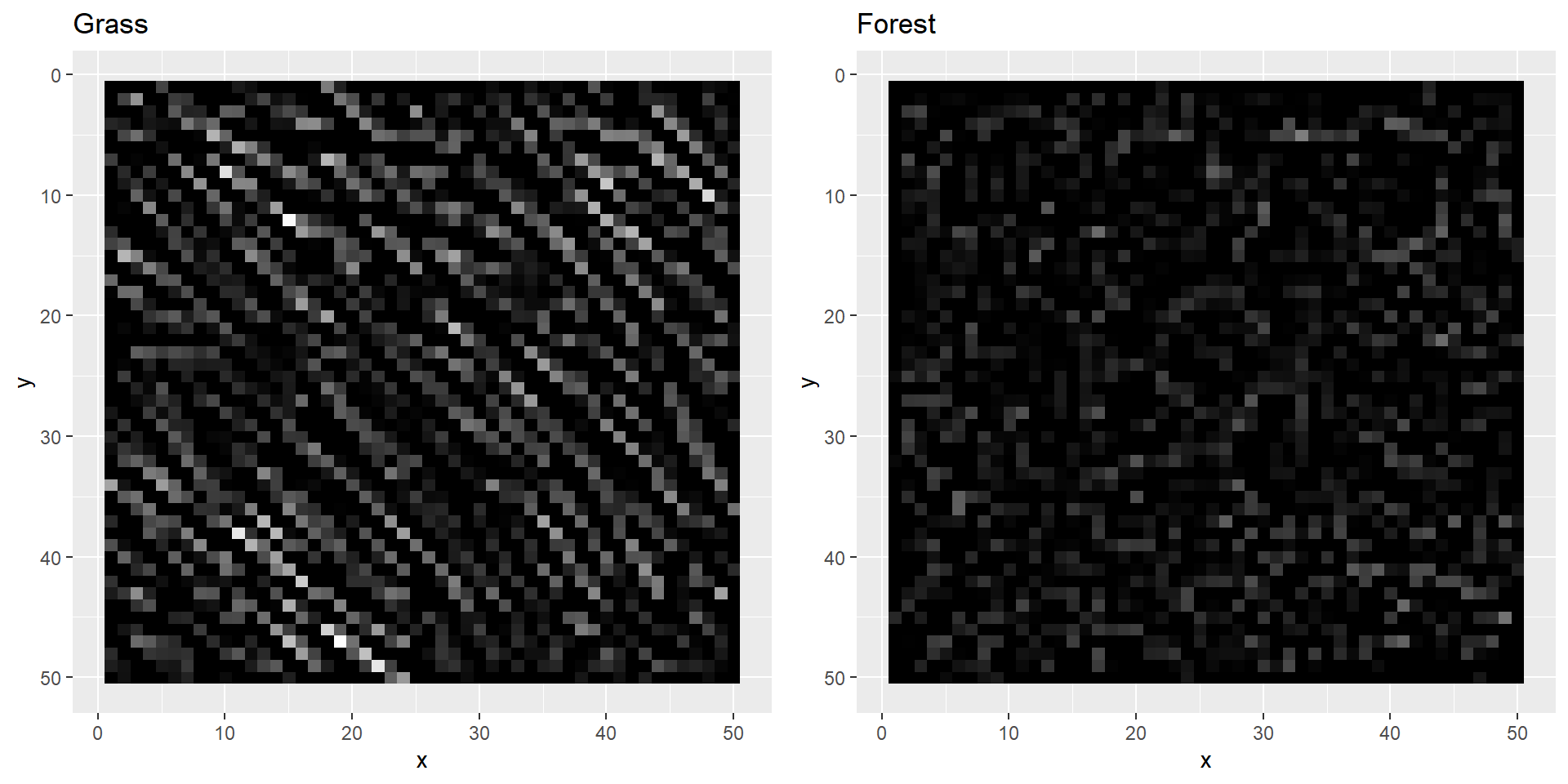
grass3[grass3 < 0] <- 0
forest3[forest3 < 0] <- 0
plotBoth(grass3, forest3)
As you can probably see, our filters highlighted the edges of our two images. Just as we hoped, the grass image lights up much more than the forest image. We can now try to use the computed values to try and distinguish both images. However, for that we need some more layers.
5.3 Max pooling
Another very common layer is a pooling layer, often placed after a convolution layer. This layer is quite similar as a convolution layer, again using a sliding window approach. The idea behind a pooling layer is to reduce the size of the convolved images through down-sampling. In contrast to the convolution layer, the pooling layer often uses a larger window that moves through the image with larger and non-overlapping strides (to make sure the pooled image is substantially smaller than its input). Most of the time the maximum value per window is returned, hence the name: max pooling.
To reduce the noise and extract the most important patterns from the image, which also makes sure it is easier to compare various images with each other that differ in orientation. Furthermore, this again makes the computation and fitting of your CNN much more efficient.
We can create a function that applies the max pooling:
maxPool <- function(im, size, stride) {
pool <- as.cimg(matrix(rep(NA_real_, (dim(im)[1]/stride * dim(im)[2]/stride)),
ncol = dim(im)[2]/stride))
for(i in seq_along(pool[1,])) {
for(j in seq_along(pool[,1])) {
pool[i,j,1,1] <- max(im[((i-1)*stride+1):(i*size),
((j-1)*stride+1):(j*size),
1,
1])
}
}
return(pool)
}There are already no zeroes left in our data, so applying a max pooling will not result in any zeroes as well.
grassPool1, forestPool1 etc. grassPool1 <- maxPool(grass1, size = 5, stride = 5)
grassPool2 <- maxPool(grass2, size = 5, stride = 5)
grassPool3 <- maxPool(grass3, size = 5, stride = 5)
forestPool1 <- maxPool(forest1, size = 5, stride = 5)
forestPool2 <- maxPool(forest2, size = 5, stride = 5)
forestPool3 <- maxPool(forest3, size = 5, stride = 5)
plotBoth(grassPool1,forestPool1)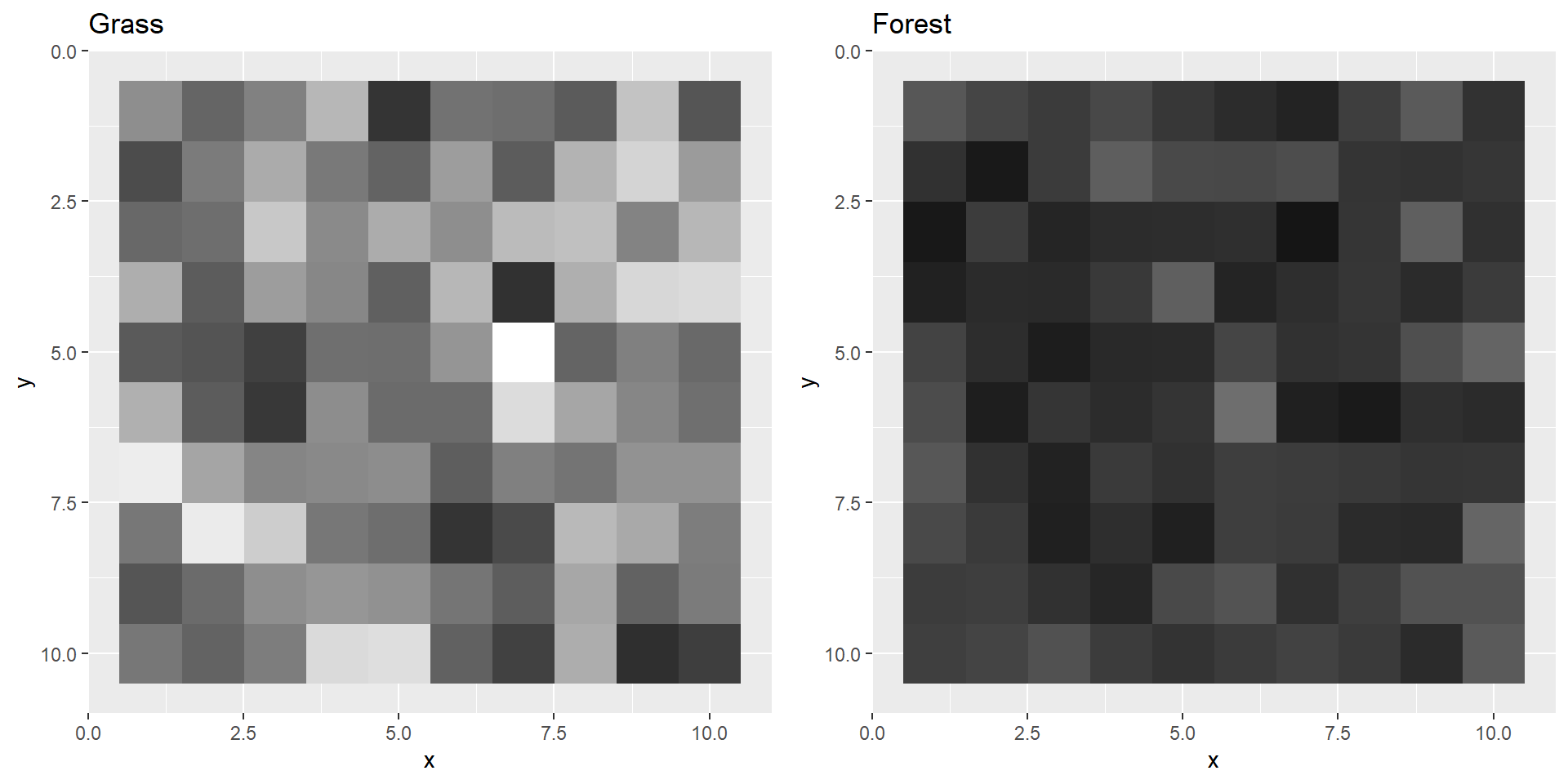
plotBoth(grassPool2,forestPool2)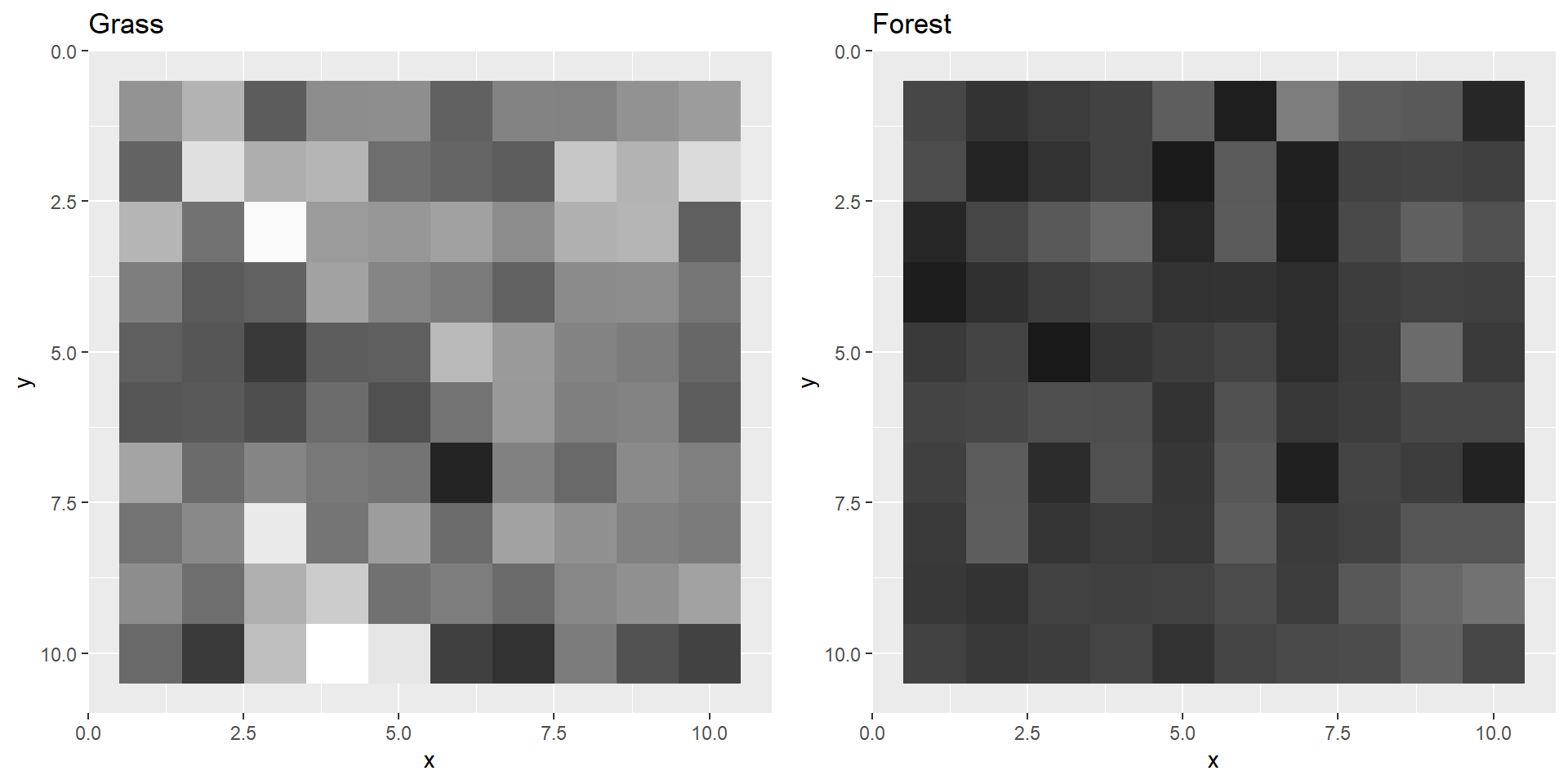
plotBoth(grassPool3,forestPool3)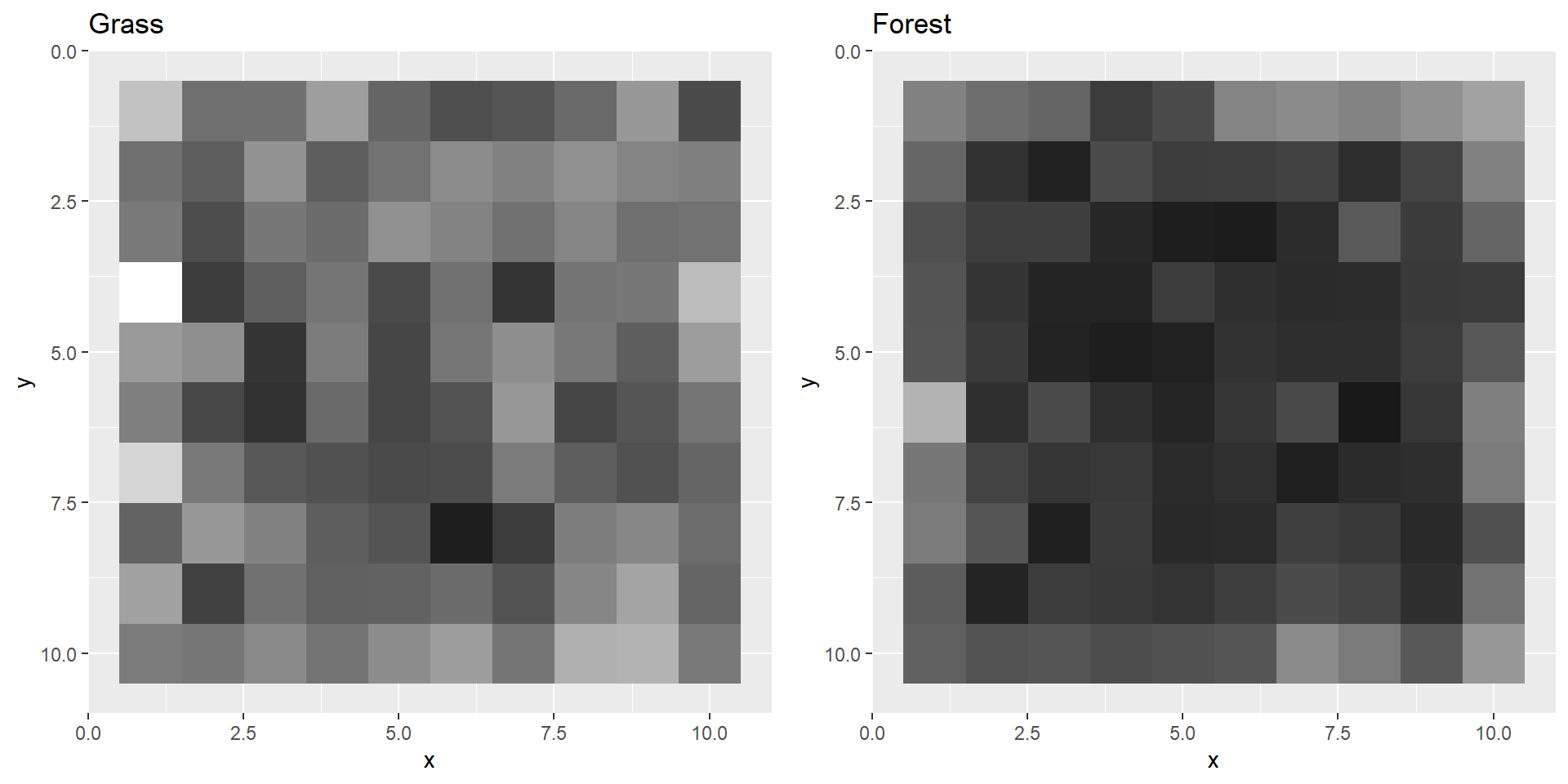
In actual CNNs there are usually multiple convolution, activation and pooling layers after each other. The more layers, the “deeper” your neural network becomes. Deep neural nets are able to detect more difficult patterns. CNNs with 50 layers are for example very common. For our example these few layers will probably suffice.
5.4 Flattening
After the last pooling layer we have finished the feature learning
part of the CNN and now arrive at the final part: the actual
classification. In order to perform the classification we need to treat
the pooled images as feature vectors, therefore we need to “flatten” our
2D images into 1D vectors. This can be performed easily in R with the
as.vector function, name them grassFlat1,
forestFlat1 etc. After you’ve flattened all the 6 pooled
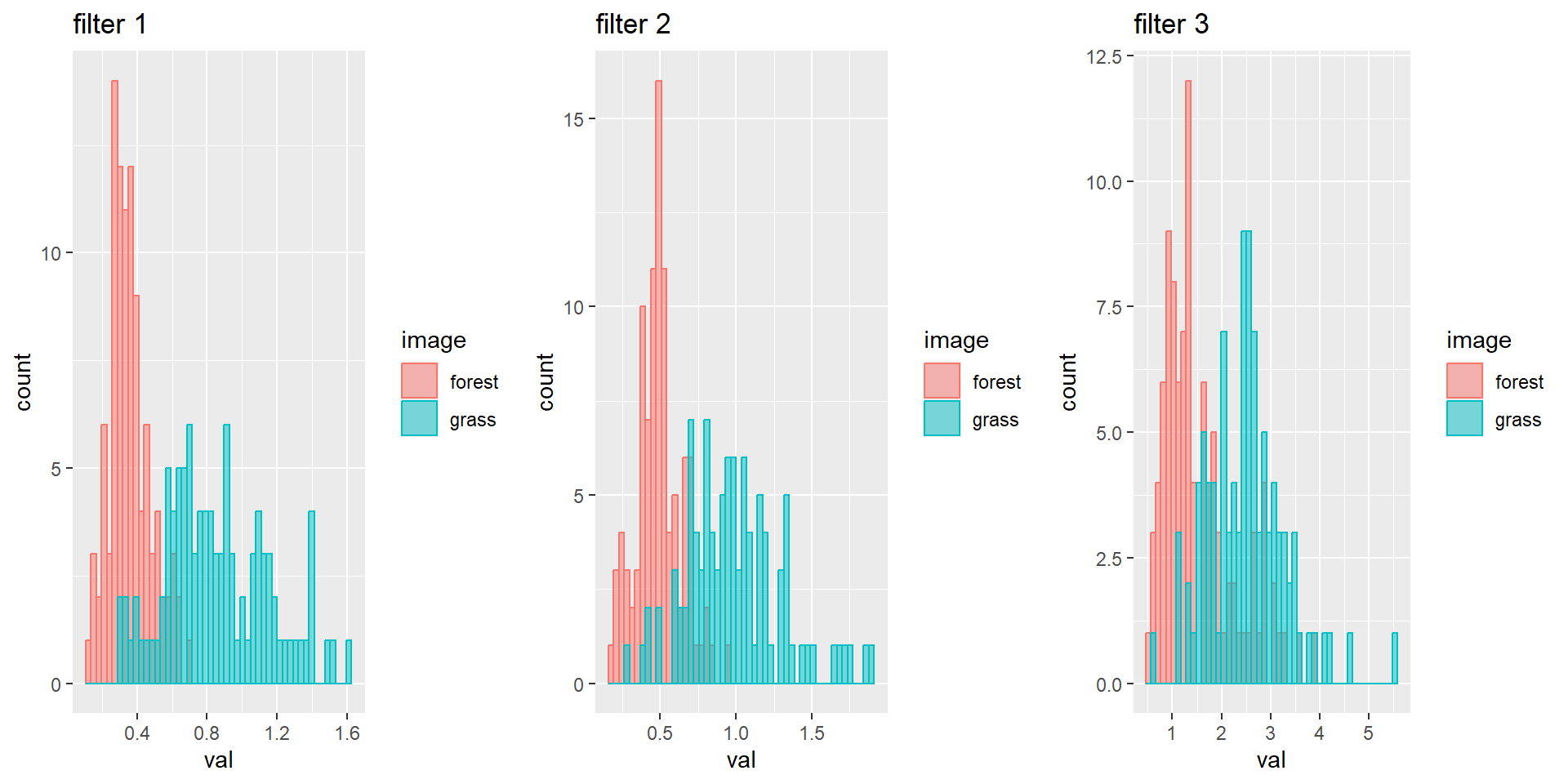
matrices, create 3 histograms of the grass and forest image combined per
filter:
# Convert to vectors
grassFlat1 <- as.vector(grassPool1)
forestFlat1 <- as.vector(forestPool1)
grassFlat2 <- as.vector(grassPool2)
forestFlat2 <- as.vector(forestPool2)
grassFlat3 <- as.vector(grassPool3)
forestFlat3 <- as.vector(forestPool3)
# Merge to tibbles
Flat1 <- tibble(val = list(grassFlat1, forestFlat1),
image = c("grass","forest")) %>%
unnest(val)
Flat2 <- tibble(val = list(grassFlat2, forestFlat2),
image = c("grass","forest")) %>%
unnest(val)
Flat3 <- tibble(val = list(grassFlat3, forestFlat3),
image = c("grass","forest")) %>%
unnest(val)
# Plot
p1 <- Flat1 %>%
ggplot(aes(x = val, color = image, fill= image)) +
geom_histogram(position = "identity", alpha = 0.5, bins = 50) +
ggtitle("filter 1")
p2 <- Flat2 %>%
ggplot(aes(x = val, color = image, fill = image)) +
geom_histogram(position = "identity", alpha = 0.5, bins = 50) +
ggtitle("filter 2")
p3 <- Flat3 %>%
ggplot(aes(x = val, color = image, fill = image)) +
geom_histogram(position = "identity", alpha = 0.5, bins = 50) +
ggtitle("filter 3")
grid.arrange(p1, p2, p3, nrow = 1)The grass image has on average much higher values than the forest image for every filter.
5.5 Fully connected
After the flattening layer, all nodes are combined with a fully
connected layer. This fully connected layer is actually a regular
feed-forward neural network in itself. The output of this fully
connected layer is a value for each class the CNN is trained to predict
(in our case grass and forest). In reality this fully connected layer
can become very complex, and have hidden fully connected layers prior to
it. However, as we’ve already seen in the histograms, our images are
easily distinguishable. So now let’s assume that we have zero hidden
layers and directly connect the flattening layer to the output layer.
Also assume that all weights connecting the nodes of the flattening to
the grass output node have a value of 0.2 and those to the
forest output node have a value of 0.1, and the bias term
for the grass output node is 0 and for the forest output
node 25. You can compute the score for both classes by
simply using the sum of the three flattened vectors and then multiplying
it with the corresponding weight and summing it with the bias term.
# Set weight and bias values
grassWeights <- .2
forestWeights <- .1
grassBias <- 0
forestBias <- 25
# Compute output values for each image and output node combination
grass_grassScore <- sum(c(grassFlat1, grassFlat2, grassFlat3))*grassWeights + grassBias
grass_forestScore <- sum(c(grassFlat1, grassFlat2, grassFlat3))*forestWeights + forestBias
forest_grassScore <- sum(c(forestFlat1, forestFlat2, forestFlat3))*grassWeights + grassBias
forest_forestScore <- sum(c(forestFlat1, forestFlat2, forestFlat3))*forestWeights + forestBiasFor every image the CNN computes the probability for both the grass and the forest class. With two images this results in four values.
5.6 Activation
Finally, after classification in the fully connected layer, the class probabilities can now be computed for every image. For this we use again an activation function, just like the ReLU function. However, at the end of the CNN a Softmax activation layer is often used. This activation function has the nice property that you can consider the output values as probabilities (values between 0-1) and it scales well with many classes, so that the class with the largest value gets a proportionally much higher value than the other classes. The Softmax function is: \(\frac{e^{x_i}}{\sum^n_{j=1} e^{x_j}}\), where \(x_i\) is the value of class \(i\) of the total of \(n\) classes that the CNN is trained for. Now compute the grass and forest probability yourself for both images.
# Softmax function
grass_grassProb <- exp(grass_grassScore) / sum(exp(grass_grassScore), exp(grass_forestScore))
grass_forestProb <- exp(grass_forestScore) / sum(exp(grass_grassScore), exp(grass_forestScore))
forest_grassProb <- exp(forest_grassScore) / sum(exp(forest_grassScore), exp(forest_forestScore))
forest_forestProb <- exp(forest_forestScore) / sum(exp(forest_grassScore), exp(forest_forestScore))
# Show values
matrix(c(grass_grassProb, grass_forestProb,
forest_grassProb, forest_forestProb),
ncol = 2,
dimnames = list(image = c("grass","forest"), # Row label and names
probability = c("grass","forest"))) # Col label and names## probability
## image grass forest
## grass 1.000000e+00 0.3023498
## forest 1.047841e-08 0.6976502The probabilities per class depend on the values of the other classes. This means that two CNNs that are trained to detect forest with the same input data, but differ in the other classes that they are trained to detect, will most likely return different probabilities for the forest class on the same image.
6 Recap
During this practical you have taken a look under the hood of a CNN to see what happens when it predicts the class probabilities of images. Hopefully you have now a better feeling about how a CNN works and about its philosophy. Furthermore, you’ll probably also be pleased to know that from now on all the convolution, pooling, flattening, connecting and activation layers will be computed for you with some very simple functions in only a few lines of code. Something to look forward to…
An R script of today’s exercises can be downloaded here